Evaluate generator quality
In MOSTLY AI, each trained generator is evaluated with an auto-generated report with the quality metrics listed below.
- accuracy
- privacy-preservation
- correlations
- distributions
- coherence (only for linked tables)
- similarity
Generator details page
All generator quality metrics are available on the generator details page, which you can access by opening a generator from the Generators page.
Accuracy
Each generator’s overall Accuracy metric measures how effectively the generator has learned the characteristics and general patterns of the original data. The higher the overall accuracy percentage, the better.
The generator Accuracy is an average of the accuracies of all AI models in the generator. For generators with a single AI model, the generator and model accuracies are the same.

The accuracy of an AI model is an aggregated statistic that is the mean of the univariate accuracy, the bivariate accuracy, and (only for linked tables) the coherence of the model. The accuracy of each model is available in the Data insights section.
You can find the univariate, bivariate, and coherence metrics for each model in its Model report.

A generator includes a separate AI model for each table, and for each language column configured to use the Language/Text encoding type. For example, a dataset with two tables and one language column will have a total of 3 AI models.
Each AI model has a separate Model report that includes detailed quality metrics.
Privacy
MOSTLY AI generates synthetic data in a privacy-safe way. The privacy of data subjects is protected as a result of the privacy-protection mechanisms that are in place for every generated synthetic dataset. Every time you train a new generator, MOSTLY AI trains AI models that learn only the general patterns of the original dataset and never memorize data points. The AI models are then able to generate data with random draws which is a process that ensures that no 1:1 relationship exists between the original and synthetic datasets. For more information, see Privacy-protection mechanisms.
In addition, for each AI model MOSTLY AI calculates the distances that synthetic samples have from the training records and also their distances from holdout records (as reference). For details, see the Distances section.
Distances
The Distances are a privacy metric that shows the average distances calculated between synthetic samples and their nearest neighbors from the training data, on one side, and between the synthetic samples and their nearest neighbors from the holdout data, on the other side (for reference).
To calculate the distances, 10% from the original data is randomly drawn into a holdout dataset. The Distance to Closest Record metric is then calculated like so and averaged for each table.
- DCR(S,T) - the distances between synthetic samples and their nearest neighbors from the training dataset
- DCR(S,H) - the distances between synthetic samples and their nearest neighbors from the holdout dataset (appears in light gray)
To gauge the privacy-preservation qualities of a generator, the generated synthetic samples should be as close to their nearest training neighbors as they are close to their nearest holdout neighbors (the data not seen during training).

The full distribution of the distances is visualized as part of the Model report. See Distances in the Model report.
Technical reference
The Distances metric is calculated based on L2 distances between samples. Each sample is converted into JSON format and is then mapped to a 384-dimensional vector space with the all-MiniLM-L6-v2 model so that the calculation takes into account semantic similarities. With this, the distances are applicable to both tabular mixed-type data as well as any unstructured text columns that you use to fine-tune LLMs.
Model report
For each model in a generator, you can open its Model report and view its metrics in detail. To open, click Model in the Reports column under Data insights.
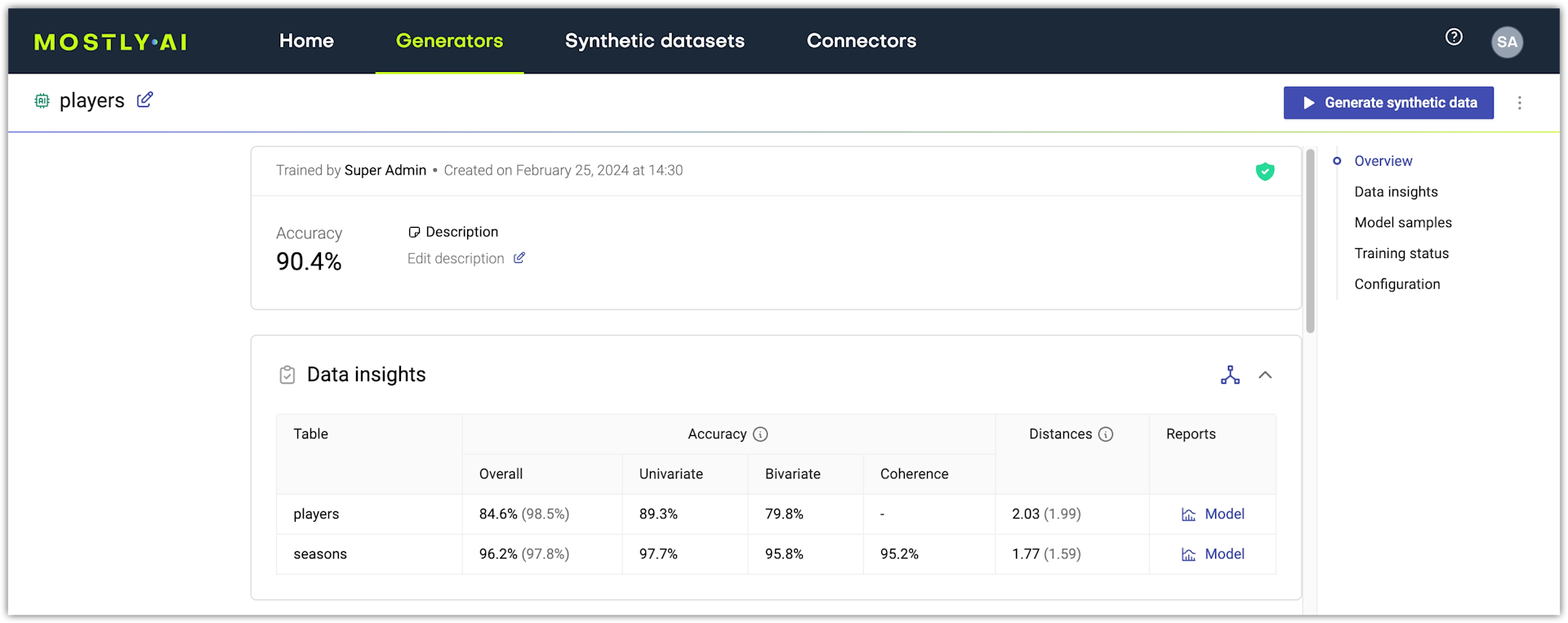
MOSTLY AI generates a Model report for each model in a generator and a Data report for each model when you generate a synthetic dataset.
The Data report is especially important when you use data augmentation features, such as Rebalancing. For example, when you use Rebalancing, the changes in the distribution of the synthetic data will be visible only in the Data report. For more information, see Evaluate synthetic data quality.
Each Model report contains a breakdown and visualization for the following generator quality metrics:
- Correlations
- Univariates
- Bivariates
- Coherence (linked tables only)
- Accuracy
- Distances
To reduce computational time, the model report is calculated on a maximum of 100,000 samples that are randomly selected from the original and synthetic data. If smaller, the entire dataset is used.
Overview of model quality metrics
At the top of the model report, you can find information about the model: when it was generated, the number of samples in the original table, the number of synthetic samples, and the generator ID.
You will also find three cards with quality metrics for Accuracy, Similarity, and Distances.
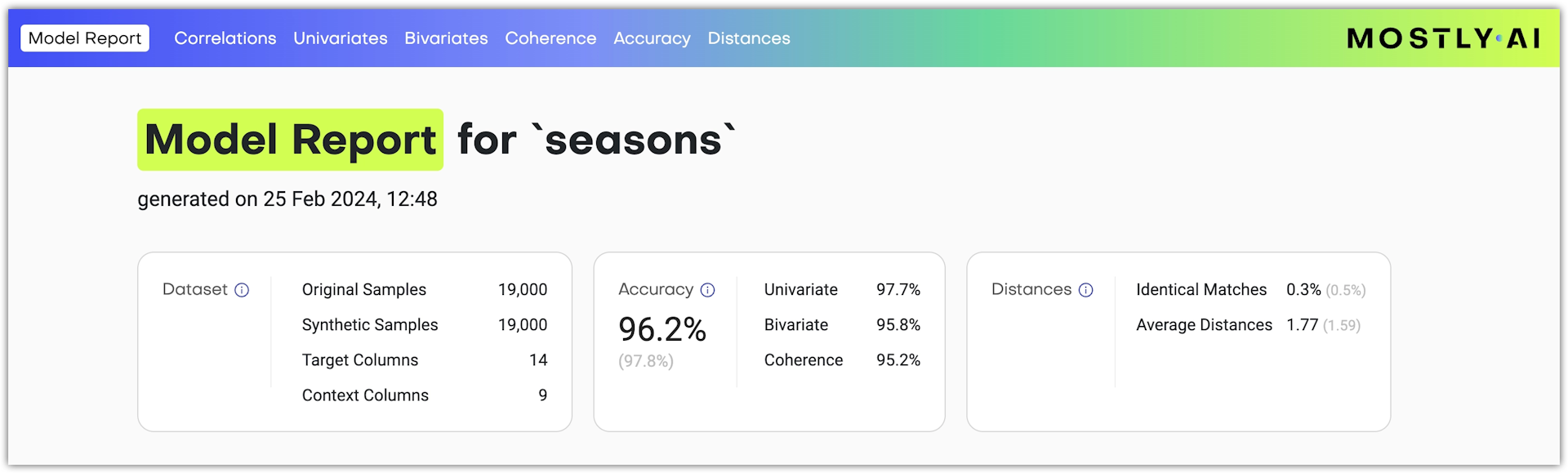
Accuracy metrics in the overview
| Accuracy metric | Description |
|---|---|
| Accuracy | The overall accuracy of the model. It shows how well synthetic data generated with the model captures the characteristics of the training data. For reference, the accuracy of the synthetic data when compared to the holdout data appears in light gray. |
| Univariate | The overall accuracy of the model’s univariate distributions. An aggregated statistic that shows the mean of the univariate accuracies of all columns. |
| Bivariate | The overall accuracy of the model’s bivariate distributions. An aggregated statistic that shows the mean of the bivariate accuracies of all columns. |
| Coherence | (Only for linked tables) The temporal coherence of time series data between the synthetic and training data as well as the preservation of the average sequence length (or the average number of linked table records that are related to a subject table record). |
Similarity metrics in the overview
| Similarity metric | Description |
|---|---|
| Cosine Similarity | The Cosine similarity explains how similar the synthetic data is to the training data. To calculate it, we first represent the synthetic and training datasets as vectors in an embedding space, and then find their centroids. Once the centroids are identified, the similarity is determined by measuring the cosine distance between the two centroid vectors. The closer the value is to 1, the higher the similarity between the synthetic dataset and the training samples, indicating higher quality. The similarity between the training and holdout datasets is also calculated and displayed in light gray for comparison. We expect these similarities to be close since we want the synthetic dataset to be as close as the holdout dataset to the training data. |
| Discriminator AUC | The Discriminator AUC shows the area under the curve of a classifier trained to distinguish between the training and synthetic embeddings. High-quality synthetic data should be indistinguishable from the original data. Therefore, we expect this value to be closer to 50%, indicating that the discriminator has only a 50% probability of correctly identifying whether the data is synthetic or real, which suggests the synthetic data closely resembles the original. Values between 50% and 60% indicate high-quality synthetic data. For comparison, the same metric is also calculated between the training and holdout datasets and displayed in light gray. |
Distances metrics in the overview
| Distances metric | Description |
|---|---|
| Identical Matches | An identical match is the special case of the distance measure being zero. In such a case, two records would share the same values across all columns. But also here, the occurrence of identical matches only represents a privacy issue if and only if it is more prevalent than within the training data itself. If the training dataset has identical matches, we can expect to see a similar number (but not significantly more) of identical matches in the synthetic data. |
| Average Distances | The average distances calculated between the synthetic records and their nearest neighbors from the training dataset used for this model. For reference, the average distances between the synthetic records and their nearest neighbors from the holdout dataset appear in light gray. |
Correlations
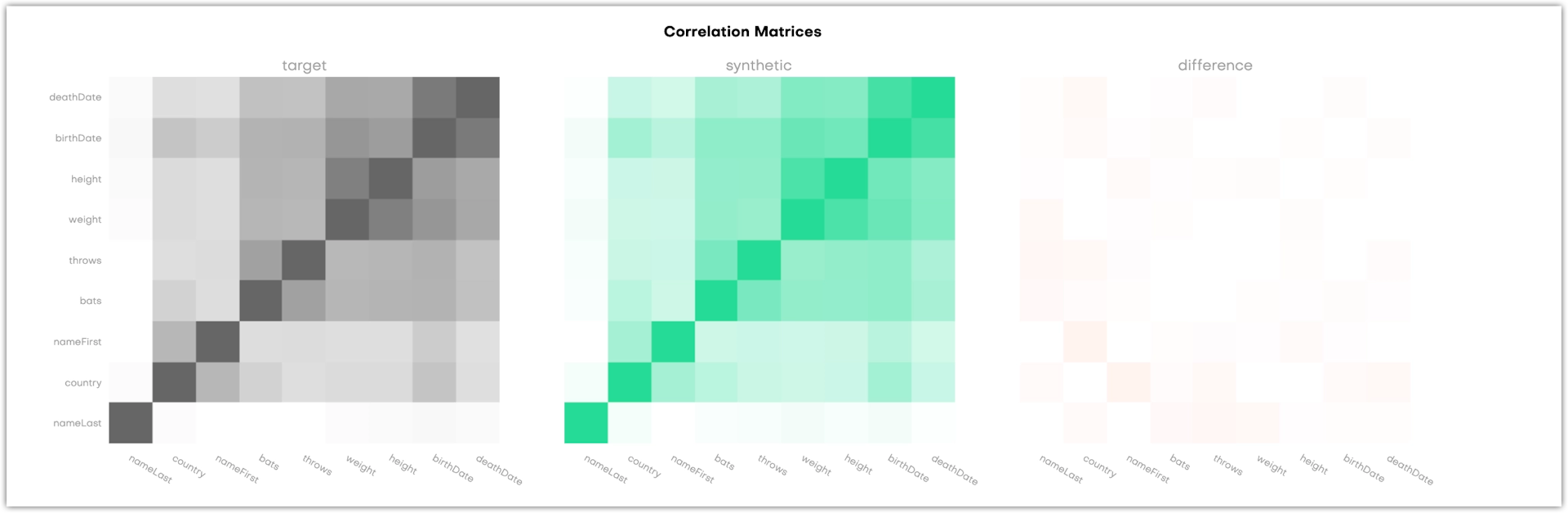
The Correlations section shows three correlation matrices. They provide a way to assess whether the synthetic dataset retained the correlation structure of the original data set. This gives you an additional way to assess the quality of the synthetic data, but does not have an impact on the calculated overall accuracy score.
Both the X and Y-axis refer to the columns in the table that is evaluated, and each cell in the matrix correlates to a variable pair: the more two variables are correlated, the darker the cell becomes. This is obvious in the dark 45 degree diagonal which shows the correlations of single variables with themselves. Naturally, their correlation coefficient is 1. The third matrix shows the difference between the original and the synthetic data.
For subject tables, the charts display all columns.
For linked tables, the charts display the correlations between all columns as well as the correlations between each column and the Sequence Length.
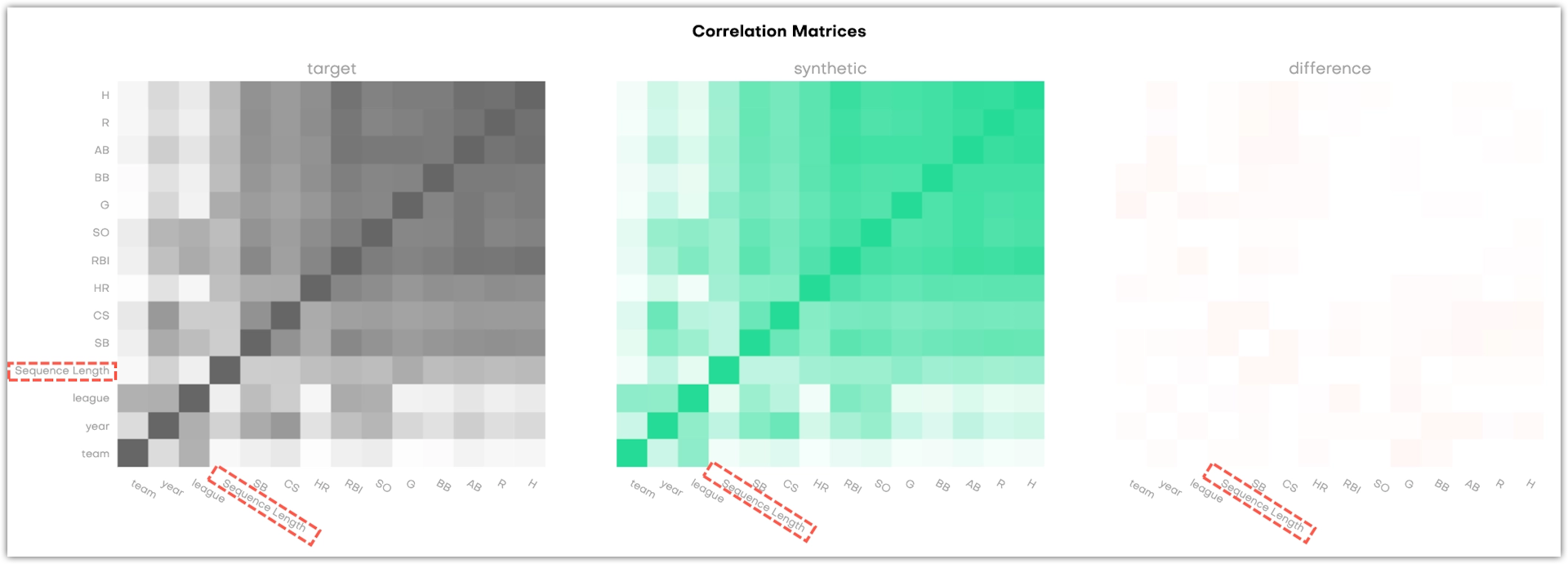
Technical reference
The correlations are calculated by binning all variables into a maximum of 10 groups. For categorical columns, the 10 most common categories are used and for numerical columns, the deciles are chosen as cut-offs. Then, a correlation coefficient Φκ is calculated for each combination of variable pairs. The Φκ coefficient provides a stable solution when combining numerical and categorical variables and also captures non-linear dependencies. The resulting correlation matrix is then color-coded as a heatmap to indicate the strength of variable interdependencies, once for the actual and once for the synthetic data with scaling between 0 and 1.
Details about the Φκ coefficient can be found in the following paper: A new correlation coefficient between categorical, ordinal and interval variables with Pearson characteristics
Univariates
Univariate distributions describe the probability of a variable having a particular value. You can find four types of plots in this section of the QA report: categorical, continuous, and datetime. A Sequence Length plot is also available if your generator includes a linked table.
For each variable, there’s a distribution and binned plot. These show the distributions of the original and the synthetic dataset in black and green, respectively. The percentage next to the title shows how accurately the original column is represented by the synthetic column.
You can search by column name to find a univariate chart.
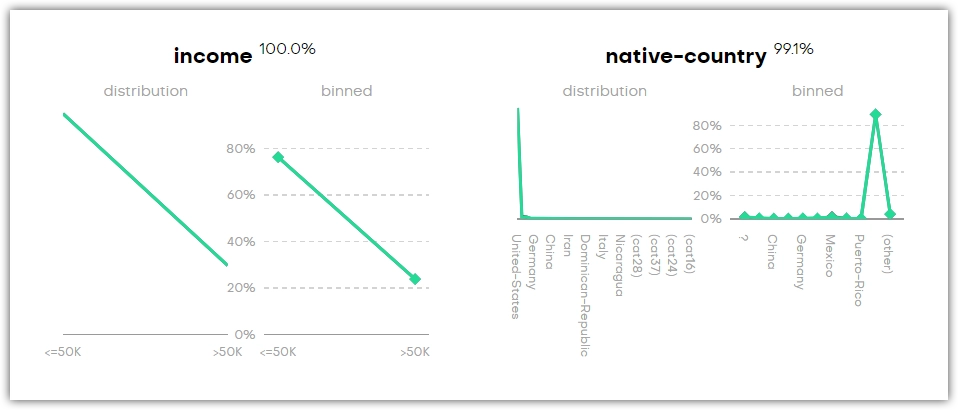
You may find categories that are not present in the original dataset (for example, _RARE_). These categories appear as a means of rare category protection, ensuring privacy protection of subjects with rare or unique features.
Technical reference
All variables are binned into a maximum of 10 groups. For categorical columns, the 10 most common categories are used and for numerical and datetime columns, the deciles are chosen as cut-offs. One additional group is used to show empty values: (empty) for categorical and (n/a) for numerical and datetime columns. This presented accuracy is the Manhattan distance (L1) calculated on the binned datasets.
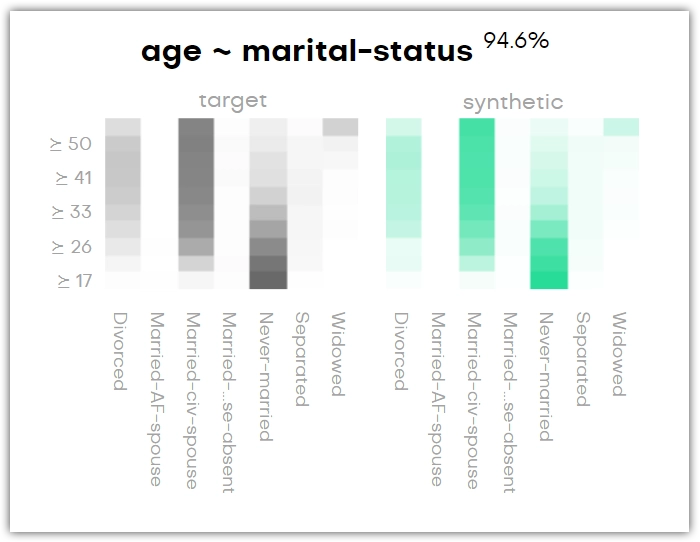
Bivariates
Bivariate distributions provide a metric of the conditional relationship between the content of two columns in your original dataset and that relationship is preserved in the synthetic dataset.
For each variable pair, there is an original and a synthetic plot. These show the relationships of the variables in the original and the synthetic dataset in black and green, respectively. Again, the percentage next to the title shows how accurately the original column is represented by the synthetic column.
The bivariate distribution below shows, for instance, that the age group of forty years and older is most likely to be married, and anyone below thirty is most likely to have never been married. You can see that this is the same in the synthetic dataset.
If it’s a QA report for a linked table, then you can find the plots with the context table’s columns by looking for context:[column-name]. The word context here refers to either the subject table or another linked table with which this linked table has been synthesized.
You can search by column name to find a bivariate chart.
You may find categories that are not present in the original dataset (for example, _RARE_). These categories appear as a means of rare category protection, ensuring privacy protection of subjects with rare or unique features.
Technical reference
All variables are binned into a maximum of 10 groups. For categorical columns, the 10 most common categories are used and for numerical and datetime columns, the deciles are chosen as cut-offs. One additional group is used to show empty values: (empty) for categorical and (n/a) for numerical and datetime columns.
In the downloadable HTML, only a selection of bivariate plots are shown, half of which are the most accurate and the other half the least accurate.
Coherence (linked tables only)
Coherence charts compare original and synthetic time-series data and their inherent correlations. A coherence chart is a bivariate plot of a column of data. The data from the column is copied into two separate columns, where the first column contains the sequence of earlier events and the second columns contains the sequence of later events. You can use coherence charts to check the probability of one type of event being followed by another.
Coherence charts are available only for linked tables. You can review the coherence of linked tables on the Coherence section of the Model report and Data report.
To interpret coherence charts, you can review the following example where a color with a higher saturation indicates higher probability that an event from a Y-axis event is followed by an X-axis event.

Accuracy
The Accuracy section is a summary of all Univariate and Bivariate distributions. It displays a table with all variables from the original dataset, the second column and third column of which list the respective univariate and bivariate accuracies.

At the bottom is an Accuracy Matrix that shows the bivariate accuracies between pairs of variables. You can also find these values in the respective Bivariate distribution charts. The diagonal values (bottom left to top right) of the chart that only belong to one variable are the univariate accuracies of that variable.

How accuracy is calculated
The accuracy of synthetic data can be assessed by measuring statistical distances between the synthetic and the original data. The metric of choice for the statistical distance is the total variation distance (TVD), which is calculated for the discretized empirical distributions. Subtracting the TVD from 100% then yields the reported accuracy measure. These are being calculated for all univariate and all bivariate distributions. The latter is done for all pair-wise combinations within the original data, as well as between the context and the target. For sequential data, an additional coherence metric is calculated that assesses the bivariate accuracy between the value of a column, and the succeeding value of a column. All of these individual-level statistics are then averaged across to provide a single informative quantitative measure. The full list of calculated accuracies is provided as a separate downloadable file.
Similarity
The similarity plots represent how the training, synthetic, and holdout datasets compare to each other in terms of their distributions. The similarity metrics are calculated in a multi-dimensional embedding space and then projected into a 2D space for easier visualization.

The principal components displayed on the X and Y axes are combinations of the original dimensions. Think of them as new dimensions that capture the most significant variability in the data.
The black dots represent the centroids of each dataset, while the colorful areas represent the distribution of the data points. The more saturated areas indicate regions with a higher concentration of data points.
A high-quality synthetic dataset should resemble closely the original data in terms of distribution. In this context, we expect the shapes and saturations of the green layers, which represent the synthetic data, to be similar to those of the training data, which appears in blue.
Additionally, the centroids’ similar positions indicate that the overall distribution of the synthetic data resembles closely the training data.
The holdout data provides a benchmark for comparison. The synthetic dataset should align closely with both the training and holdout data, confirming its quality and generalizability.
Distances
The full distribution of the distances to closest records appears at the end of the Model report.
The distances of the synthetic samples to the training samples are displayed in green, and the distances of the synthetic samples to the holdout samples are displayed in gray.
In the chart, you can ascertain that the synthetic samples are as close to the original training samples as they are to the holdout samples (which serves as a reference).

Disable Model reports
Model reports provide rich insights into the quality of the synthetic data generated by a model. However, the generation of Model reports take time.
By default, a Model report is enabled and generated for each model in a generator (this includes both tabular and language).
Steps
To disable the Model report for a model, select Off from the model’s Model report section.

Result
After the training or fine-tuning of all models in the generator completes, come the steps to finalize each model and finalize the generator. During those steps, the Model reports are not generated and the finalization is, therefore, faster.
Any disabled Model reports will not be available for the generator as well as for any synthetic datasets generated with the generator.
Get quality metrics with the Python SDK
The Python SDK provides direct access to the metrics of each generator. Get a generator with mostly.generators.get('GENERATOR_ID') and then access the metrics with g.tables[0].tabular_model_metrics (for tabular models) and g.tables[0].language_model_metrics (for language models).
g.tables[0].tabular_model_metrics- returns the metrics of the first table model in the generator. Increment0for each subsequent model in the generator.g.tables[0].language_model_metrics- returns the metrics of the language model of the first table in the generator (available when a text column has the Language/Text encoding type).
g = mostly.generators.get('GENERATOR_ID')
g.tables[0].tabular_model_metricsThe following is an example of the model metrics obtained with the Python SDK.
{
'accuracy': {
'overall': 0.946,
'univariate': 0.958,
'bivariate': 0.934,
'coherence': None,
'overall_max': 0.984
},
'distances': {
'dcr_training': 0.075,
'dcr_holdout': 0.077,
'dcr_original': None,
'dcr_synthetic': None
},
'similarity': {
'cosine_similarity_training_synthetic': 0.99995,
'cosine_similarity_training_holdout': 0.99998,
'discriminator_auc_training_synthetic': 0.531,
'discriminator_auc_training_holdout': 0.506
}
}To get the language model metrics (if that table model has a column with the Language/Text encoding type), use the following code.
g.tables[0].language_model_metrics{
'accuracy': {
'overall': 0.93,
'univariate': 0.956,
'bivariate': 0.904,
'coherence': None,
'overall_max': 0.936
},
'distances': {
'dcr_training': 0.491,
'dcr_holdout': 0.493,
'dcr_original': None,
'dcr_synthetic': None
},
'similarity': {
'cosine_similarity_training_synthetic': 0.99927,
'cosine_similarity_training_holdout': 0.99921,
'discriminator_auc_training_synthetic': 0.535,
'discriminator_auc_training_holdout': 0.516
}
}Each synthetic dataset also provides the metrics of its generator. So, you can get the generator metrics also by using the synthetic_dataset object.
sd = mostly.synthetic_datasets.get('SYNTHETIC_DATASET_ID')
sd.tables[0].tabular_model_metricsThe returned metrics are the same as those reported for the generator.
{
'accuracy': {
'overall': 0.946,
'univariate': 0.958,
'bivariate': 0.934,
'coherence': None,
'overall_max': 0.984
},
'distances': {
'dcr_training': 0.075,
'dcr_holdout': 0.077,
'dcr_original': None,
'dcr_synthetic': None
},
'similarity': {
'cosine_similarity_training_synthetic': 0.99995,
'cosine_similarity_training_holdout': 0.99998,
'discriminator_auc_training_synthetic': 0.531,
'discriminator_auc_training_holdout': 0.506
}
}